复现 A Tutorial on Linear and Differential Cryptanalysis中差分分析的例子

前言

黑历史++😢😢😢

差分分析

什么是差分分析呢？其实简单来说，就是考察明文的某一或某些位取反对密文的影响，所以这里的差分，实质就是异或的意思。其实感觉差分分析的过程和线性分析是基本一致的，所以这个博客我就写简单一点，实在记不住了还可以翻阅上一篇博客。虽然上一篇也不怎么详细（）

Sbox拟合

与线性分析一致，我们不得不对sbox进行拟合。同样的，对于输入的每一种可能的差分，我们穷举所有的输入1（输入2=输入1$\oplus$输入差分）并记录由此带来的输出差分值（输出差分=输出1$\oplus$输出2），计算出输入差分和输出差分对应的概率关系。通过16*16的256次计算，我们就可以整理出一张sbox的拟合表格。

子密钥分析

同样的，我们选取概率较大的路径，可以得到明文对的一个差分和一个倒数第二轮输出的差分之间的概率，在论文中，选取的是$\Delta P = [0000\ 1011\ 0000\ 0000]$和$\Delta U4 = [0000\ 0110\ 0000\ 0110]$，概率是$\frac{27}{1024}=0.0264$。

同样的我们穷举最后一轮相关联的密钥$k_2$和$k_4$，通过倒推得到$U4$，最后计算出当$\Delta P$成立时$\Delta U4$成立的概率即可。

由于我们选择的是高概率路径，所以最后成立概率最高的密钥就大概率是我们要找的密钥。

复现结果

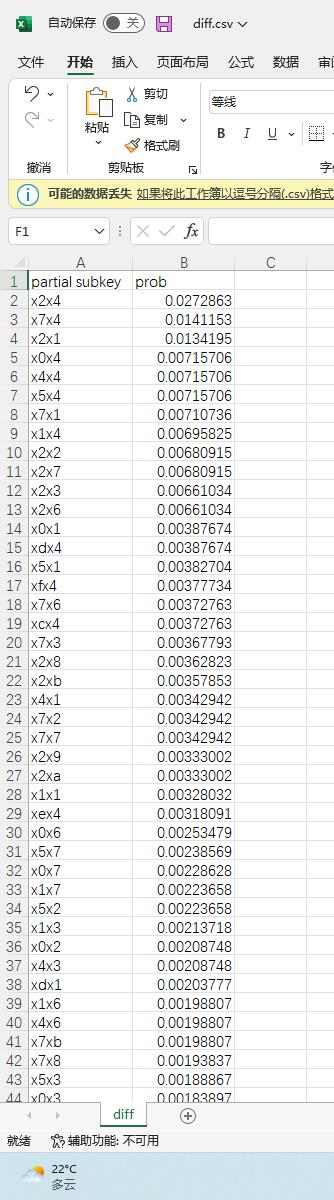
其中子密钥用16进制表示，x表示未知（即和例子的路径无关）。

可见$k_2=2$且$k_4=4$的概率远超其他密钥组合，而且概率$0.0272863$与理论$\frac{27}{1024}=0.0264$非常接近。

复现代码

#include "structure.hh"

// \delta P  = [0000 1011 0000 0000]
// \delta U4 = [0000 0110 0000 0110]

const char* FileNamePlain = "plaintexts.hex";
const char* FileNameCipher = "ciphertexts.hex";
const char* FileNameCsv = "diff.csv";
ifstream fp, fc;
ofstream fcsv;
int pcPair[1<<16]; // use -1 stands for undefined
const u16 deltaP = 0b0000101100000000;
const u16 deltaU4 = 0b0000011000000110;

inline u16 getU4(u16 _C, u16 key)
{
    _C = key_mixing(_C, key);
    _C = substitution(_C, SBOX_INV);
    return _C;
}

int main()
{
    fp.open(FileNamePlain, ios::binary | ios::in);
    fc.open(FileNameCipher, ios::binary | ios::in);
    memset(pcPair, 0xff, sizeof pcPair);

    int num = 0;
    for(;;)
    {
        u16 P, U;
        if(!fp.read((char*)&P, 2)) break;
        if(!fc.read((char*)&U, 2)) break;
        P = P << 8 | P >> 8;
        U = U << 8 | U >> 8;
        if(!~pcPair[P]) num++;
        pcPair[P] = U;
        // cerr << hex << P << "->" << U << endl;
        // if(num == 100) break;
    }
    cerr <<  "num = " << num << endl; // 有效明密文对个数（剔除重复）

    fp.close();
    fc.close();

    fcsv.open(FileNameCsv, ios::out);
    fcsv << "partial subkey" << "," << "prob" << endl;

    for(u16 k2 = 0; k2 < 16; k2++) for(u16 k4 = 0; k4 < 16; k4++)
    {
        int sum = 0, count = 0;
        u16 key = k2 << 8 | k4;
        for(int i = 0; i < 65536; i++)
        {
            if(pcPair[i] == -1) continue;
            if(pcPair[i^deltaP] == -1) continue;
            if(i > (i ^ deltaP)) continue;
            // cerr << (!(pcPair[i] == -1) && !(pcPair[i^deltaP] == -1)) << endl;
            sum++;
            if((getU4(pcPair[i],key) ^ getU4(pcPair[i^deltaP],key)) == deltaU4)
                count++;
        }
        double prob = count * 1.0 / sum;
        fcsv << hex << "x" << k2 << "x" << k4 << "," << dec << prob << endl;
        if(!k2 && !k4) cerr << "sum = " << sum << endl; // 有效明密文对组的组数（剔除没有配对成组的）
    }

    fcsv.close();
    return 0;
}

structure.hh是我自己写的一个头文件，里面是加密解密需要用到的函数以及Sbox和permutation连线的方式。由于加密解密以及分析都需要用到这些函数，所以就放在头文件里面了。

用cpp的原因是，bluebeen告诉我cpp比python快数十倍……python分析10万组明密文对要1分钟真的难受……

因为差分分析需要符合要求的明密文对组，即明文需要满足$\Delta P$的那个式子。所以是先把涉及到的明密文对存下来（代码里面是pcPair）然后在进行统计。

在进行差分分析的复现的时候，我突然想到一个问题，为什么论文上只用了1万对明密文对，而我用了10万对才能找出答案吗？我的复现究竟是出了什么样的问题呢？

其实在上面的复现代码中，输出num和sum就已经揭晓了答案。根据输出，我的10万对明密文，只有num=5万的有效明密文对，然后再安装$\Delta P$的要求配对后，只有sum=2万组。而论文直接说的就是1万组满足$\Delta P$的明密文组。其实我也就用了两倍的数据而已。所以我的数据看起来比论文中要精确一些，但是也没有精确太多。

参考资料

[1]Heys, Howard M . A Tutorial on Linear and Differential Cryptanalysis[J]. Cryptologia, 2002, 26(3):189-221.