A 题:小蓝与钥匙
问题描述
小蓝是幼儿园的老师,他的班上有 28 个孩子,今天他和孩子们一起进行了一个游戏。
小蓝所在的学校是寄宿制学校,28 个孩子分别有一个自己的房间,每个房间对应一把钥匙,每把钥匙只能打开自己的门。现在小蓝让这 28 个孩子分别将自己宿舍的钥匙上交,再把这 28 把钥匙随机打乱分给每个孩子一把钥匙,有$28! = 28\times27\times \cdots \times1$种分配方案。小蓝想知道这些方案中,有多少种方案恰有一半的孩子被分到自己房间的钥匙(即有 14 个孩子分到的是自己房间的钥匙,有 14 个孩子分到的不是自己房间的钥匙)。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
考场思路
显然这个题分为两步,一是有14个同学分到了自己的钥匙,二是剩下的14个同学都没有分到自己的钥匙,记方案数为$Q$,则有:
$$
Q = C_{28}^{14} \cdot D_{14}
$$
其中$D_{14}$为14的全错位排列。全错位排列也称“欧拉装错信箱问题”,其计算可用容斥原理,公式如下:
$$
D_n = \sum_{i=0}^{n} (-1)^i \cdot C_n^i \cdot (n-i)!
$$
或者:
$$
D_n = n! \cdot \sum_{i=0}^{n} \frac{(-1)^i}{i!}
$$
于是有方案数$Q=1,286,583,532,342,313,400$
B 题:排列距离
问题描述
小蓝最近迷上了全排列,现在他有一个长度为 17 的排列,里面包含的元素有:abcdefghijklnopqr,即 a 至 r 中除了 m 以外的所有小写字母,这 17个字母在任何一个排列中都恰好出现一次。前面几个排列依次是:
第 1 个排列为:abcdefghijklnopqr;
第 2 个排列为:abcdefghijklnoprq;
第 3 个排列为:abcdefghijklnoqpr;
第 4 个排列为:abcdefghijklnoqrp;
第 5 个排列为:abcdefghijklnorpq;
第 6 个排列为:abcdefghijklnorqp;
第 7 个排列为:abcdefghijklnpoqr;
第 8 个排列为:abcdefghijklnporq;
第 9 个排列为:abcdefghijklnpqor;
第 10 个排列为:abcdefghijklnpqro。
对于一个排列,有两种转移操作:
1)转移到其下一个排列。如果当前排列已经是最后一个排列,那么下一个排列就是第一个排列。
2)转移到其上一个排列。如果当前排列是第一个排列,那么上一个排列就是最后一个排列。
小蓝现在有两个排列,分别为排列 A:aejcldbhpiogfqnkr,以及排列B:ncfjboqiealhkrpgd,他现在想知道,在只有上述两种转移操作的前提下,排列 A 最少转移多少次能得到排列 B。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
考场思路
显然只要知道了排列A和排列B分别是第几个排列就可以了。
因此我们使用康托展开(Cantor expansion)就可以了。若记排列$\lambda$为$a_1,a_2,a_3,\dots,a_n$,则有:
$$
X_{\lambda} = q_1 \cdot (n-1)! + q_2 \cdot (n-2)! + \cdots + q_n \cdot 0!
$$
其中$q_i$表示$a_i$在$a_i,a_{i+1},\dots,a_n$中是第$q_i$小的数,则$X_\lambda$表示排列$\lambda$是第$X_\lambda$个排列。(注:这里第几小的数和第几个排列都从0开始标号,计算会比较方便)
最后我的结果是:排列A的编号是$4,542,892,071,974$,排列B的编号是$254,081,962,595,831$,最终答案取$min{X_A - X_B + 19!, X_B - X_A} = 106,148,357,572,143$即可。
C 题:内存空间
问题描述
小蓝最近总喜欢计算自己的代码中定义的变量占用了多少内存空间。
为了简化问题,变量的类型只有以下三种:
int:整型变量,一个 int 型变量占用 4 Byte 的内存空间。
long:长整型变量,一个 long 型变量占用 8 Byte 的内存空间。
String:字符串变量,占用空间和字符串长度有关,设字符串长度为 L,则字符串占用 L Byte 的内存空间,如果字符串长度为 0 则占用 0 Byte 的内存空间。定义变量的语句只有两种形式,第一种形式为:
type var1=value1,var2=value2...;
定义了若干个 type 类型变量 var1、var2、…,并且用 value1、value2…初始化,
多个变量之间用’,’ 分隔,语句以’;’ 结尾,type 可能是 int、long 或 String。例如 int a=1,b=5,c=6; 占用空间为 12 Byte;long a=1,b=5; 占用空间为 16 Byte;String s1=””,s2=”hello”,s3=”world”; 占用空间为 10 Byte。第二种形式为:
type[] arr1=new type[size1],arr2=new type[size2]...;
定义了若干 type 类型的一维数组变量 arr1、arr2…,且数组的大小为size1、size2…,多个变量之间用’,’ 进行分隔,语句以’;’ 结尾,type 只可能是 int 或 long。例如 int[] a1=new int[10]; 占用的内存空间为 40Byte;long[] a1=new long[10],a2=new long[10]; 占用的内存空间为160 Byte。已知小蓝有 T 条定义变量的语句,请你帮他统计下一共占用了多少内存空间。结果的表示方式为:
aGBbMBcKBdB,其中 a、b、c、d 为统计的结果,GB、MB、KB、B 为单位。优先用大的单位来表示,1GB=1024MB,1MB=1024KB,1KB=1024B,其中 B 表示 Byte。如果 a、b、c、d 中的某几个数字为 0,那么不必输出这几个数字及其单位。题目保证一行中只有一句定义变量的语句,且每条语句都满足题干中描述的定义格式,所有的变量名都是合法的且均不重复。题目中的数据很规整,和上述给出的例子类似,除了类型后面有一个空格,以及定义数组时 new 后面的一个空格之外,不会出现多余的空格。
输入格式
输入的第一行包含一个整数 T ,表示有 T 句变量定义的语句。
接下来 T 行,每行包含一句变量定义语句。
输出格式
输出一行包含一个字符串,表示所有语句所占用空间的总大小。
测试样例
| 样例输入 | 样例输出 |
|---|---|
| 1 long[] nums=new long[131072]; |
1MB |
| 4 int a=0,b=0; long x=0,y=0; String s1=”hello”,s2=”world”; long[] arr1=new long[100000],arr2=new long[100000]; |
1MB538KB546B |
样例说明
样例 1,占用的空间为 131072 × 8 = 1048576 B,换算过后正好是 1MB,其它三个单位 GB、KB、B 前面的数字都为 0 ,所以不用输出。
样例 2,占用的空间为 4 × 2 + 8 × 2 + 10 + 8 × 100000 × 2 B,换算后是1MB538KB546B。
规模与约定
对于所有评测用例,1 ≤ T ≤ 10,每条变量定义语句的长度不会超过 1000。所有的变量名称长度不会超过 10,且都由小写字母和数字组成。对于整型变量,初始化的值均是在其表示范围内的十进制整数,初始化的值不会是变量。对于 String 类型的变量,初始化的内容长度不会超过 50,且内容仅包含小写字母和数字,初始化的值不会是变量。对于数组类型变量,数组的长度为一个整数,范围为:$[0, 2^{30}]$,数组的长度不会是变量。T 条语句定义的变量所占的内存空间总大小不会超过 1 GB,且大于 0 B。
考场思路
这个题,怎么说呢,几乎就是纯模拟吧大概。
首先每行的首个字符串就是类型说明,然后对于不同的类型找不同的符号就可以了。
比如int和long型,就找有多少个“,”;数组就找“int[”和“long[”;字符串就找“””就可以了。
部分代码如下:
void solve_int(const char* str)
{
while(*str)
{
if(*str == ',' || *str == ';') ans += 4;
str++;
}
}
void solve_int_arr(const char* str)
{
const char* tmp;
// const char* lst = str + strlen(str);
while((tmp = strstr(str, "int[")) != NULL)
{
tmp += 4;
int num = 0;
while(isdigit(*tmp))
{
num = num * 10 + (*tmp - '0');
tmp++;
}
str = tmp;
ans += 4 * num;
}
}
void solve_long(const char* str)
{
while(*str)
{
if(*str == ',' || *str == ';') ans += 8;
str++;
}
}
void solve_long_arr(const char* str)
{
const char* tmp;
// const char* lst = str + strlen(str);
while((tmp = strstr(str, "long[")) != NULL)
{
tmp += 5;
int num = 0;
while(isdigit(*tmp))
{
num = num * 10 + (*tmp - '0');
tmp++;
}
str = tmp;
ans += 8 * num;
}
}
void solve_String(const char* str)
{
const char* tmp;
// const char* lst = str + strlen(str);
while((tmp = strchr(str, '\"')) != NULL)
{
// fprintf("tmp=%s\n",tmp);
tmp += 1;
int num = 0;
while(*tmp != '\"')
{
num++;
tmp++;
}
str = tmp + 1;
ans += num;
}
}D 题:最大公约数
问题描述
给定一个数组,每次操作可以选择数组中任意两个相邻的元素 x, y 并将其中的一个元素替换为 gcd(x, y) ,其中 gcd(x, y) 表示 x 和 y 的最大公约数。
请问最少需要多少次操作才能让整个数组只含 1 。
输入格式
输入的第一行包含一个整数 n ,表示数组长度。
第二行包含 n 个整数 a1, a2, · · · , an,相邻两个整数之间用一个空格分隔。
输出格式
输出一行包含一个整数,表示最少操作次数。如果无论怎么操作都无法满足要求,输出 −1。
测试样例
| 样例输入 | 样例输出 |
|---|---|
| 3 4 6 9 |
4 |
规模与约定
对于 30% 的评测用例,$n ≤ 500 ,a_i ≤ 1000$;
对于 50% 的评测用例,$n ≤ 5000 ,a_i ≤ 10^6$;
对于所有评测用例,$1 ≤ n ≤ 100000 ,1 ≤ a_i ≤ 10^9$。
考场思路
可以发现,如果数列中有一个数为1,那么问题就很好解决了:答案即为非1的个数。
因此本题的关键在于如何最快的弄出一个1。
由于题目只允许相邻的两个数取gcd,所以如果找到连续k个数gcd为1的话,就可以用k-1次操作把其中一个数换为1,因此答案为:n+k-2。(当然,如果这n个数的gcd为非1,就直接输出-1即可)
于是问题化为如何找到这个最小的k。
稍微暴力的做法是,首先求两个两个的gcd,然后求三个三个的gcd(可以发现,三个数的gcd就是相邻两个gcd的gcd),依次下去,每次gcd的数目减小1,于是时间复杂度是$O(\sum_{i=1}^n i)$即$O(n^2)$(由于$a_i$并不大,所以gcd的复杂度(不超过$O(5 \lg n)$,大约就是10倍左右)就忽略了)实现大致如下:
void focus_solve()
{
int ans = n - 1;
while(!flag)
{
n--; ans++;
for(int i = 0; i < n; i++)
{
num[i] = gcd(num[i], num[i+1]);
if(num[i] == 1) {flag = true;break;}
}
}
printf("%d\n", ans);
}至于100%的数据,我使用了倍增+二分,复杂度大概是$O(40nlogn)$(倍数是gcd的复杂度),复杂度上肯定是没有问题的。大致的想法就是先预处理出从数量任意一个数起,2的整次幂个数的gcd,这里复杂度就是$O(20nlogn)$。然后对上面说的k进行二分(k最大取n),每次check遍历起点,然后用预处理的数据计算出k个数的gcd,也是$O(20nlogn)$。代码大致如下:
const int pow2[] = {1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192,16384,32768,65536,131072};
bool check(int x)
{
int logval = upper_bound(pow2, pow2 + 18, x) - pow2 - 1; // logval = log2(x)向下取整-1
for(int i = 0; i < n - x + 1; i++)
{
int l = i, r = i + x;
int _g = gcd(_gcd_2[l][logval], _gcd_2[r-pow2[logval]][logval]);
// _gcd_2就是预处理数组
if(_g == 1) return true;
}
return false;
}
void solve()
{
int max_log = upper_bound(pow2, pow2 + 18, n) - pow2;
for(int p = 0; p < max_log; p++)
for(int i = 0; i < n; i++)
{
if(p == 0) _gcd_2[i][0] = num[i];
else if (i+pow2[p-1] >= n) _gcd_2[i][p] = _gcd_2[i][p-1];
else _gcd_2[i][p] = gcd(_gcd_2[i][p-1], _gcd_2[i+pow2[p-1]][p-1]);
}
int L = 1, R = n;
while(L != R)
{
int mid = L + R >> 1;
if(check(mid)) R = mid;
else L = mid + 1;
}
printf("%d\n", n + L - 2);
}E 题:owo
问题描述
小蓝很喜欢 owo ,他现在有一些字符串,他想将这些字符串拼接起来,使得最终得到的字符串中出现尽可能多的 owo 。
在计算数量时,允许字符重叠,即 owowo 计算为 2 个,owowowo 计算为3 个。
请算出最优情况下得到的字符串中有多少个 owo。
输入格式
输入的第一行包含一个整数 n ,表示小蓝拥有的字符串的数量。
接下来 n 行,每行包含一个由小写英文字母组成的字符串 si 。
输出格式
输出 n 行,每行包含一个整数,表示前 i 个字符串在最优拼接方案中可以得到的 owo 的数量。
测试样例
| 样例输入 | 样例输出 |
|---|---|
| 3 owo w ow |
1 1 2 |
规模与约定
对于 10% 的评测用例,$n ≤ 10$;
对于 40% 的评测用例,$n ≤ 300$;
对于 60% 的评测用例,$n ≤ 5000$;
对于所有评测用例,$1 ≤ n ≤ 10^6 ,1 ≤ |s_i| ,\sum|s_i| ≤ 10^6$,其中 $|s_i|$表示字符串$s_i$的长度。
考场思路
首先肯定要能计算出每个字符串内部的owo的个数,当然这个是比较好计算的,用kmp或者直接用两个flag就能搞定。
其实是最重要的,要考虑拼接,不过好在这个owo很短,可用的拼接方式并不多,大致应该只有如下三种:
- 以ow结尾+以o开头
- 以o结尾+以wo开头
- 以o结尾+单独一个字母w+以o开头
因此我们就统计上面这些可以拼接的字符串的数量就可以了。但是需要注意的是,如果一个字符串既以ow结尾又以o开头,虽然都要计数,但是不能自己和自己拼接在一起,不仅如此,字符串也不能拼接成环。但是这个我在考试的时候想的不多,就没有考虑完全,大概是寄了,因此就不放代码了,如何实现就留给读者思考吧。
F 题:环境治理
问题描述
LQ 国拥有 n 个城市,从 0 到 n − 1 编号,这 n 个城市两两之间都有且仅有一条双向道路连接,这意味着任意两个城市之间都是可达的。每条道路都有一个属性 D ,表示这条道路的灰尘度。当从一个城市 A 前往另一个城市 B 时,可能存在多条路线,每条路线的灰尘度定义为这条路线所经过的所有道路的灰尘度之和,LQ 国的人都很讨厌灰尘,所以他们总会优先选择灰尘度最小的路线。
LQ 国很看重居民的出行环境,他们用一个指标 P 来衡量 LQ 国的出行环境,P 定义为:
$$
P = \sum_{i=0}^{n-1}\sum_{j=0}^{n-1}d(i,j)
$$
其中 d(i, j) 表示城市 i 到城市 j 之间灰尘度最小的路线对应的灰尘度的值。为了改善出行环境,每个城市都要有所作为,当某个城市进行道路改善时,会将与这个城市直接相连的所有道路的灰尘度都减少 1,但每条道路都有一个灰尘度的下限值 L,当灰尘度达到道路的下限值时,无论再怎么改善,道路的灰尘度也不会再减小了。
具体的计划是这样的:
第 1 天,0 号城市对与其直接相连的道路环境进行改善;
第 2 天,1 号城市对与其直接相连的道路环境进行改善;
…
第 n 天,n − 1 号城市对与其直接相连的道路环境进行改善;
第 n + 1 天,0 号城市对与其直接相连的道路环境进行改善;
第 n + 2 天,1 号城市对与其直接相连的道路环境进行改善;
…LQ 国想要使得 P 指标满足 P ≤ Q。请问最少要经过多少天之后,P 指标可以满足 P ≤ Q。如果在初始时就已经满足条件,则输出 0 ;如果永远不可能满足,则输出 −1。
输入格式
输入的第一行包含两个整数$n, Q$,用一个空格分隔,分别表示城市个数和期望达到的$P$指标。
接下来$n$行,每行包含$n$个整数,相邻两个整数之间用一个空格分隔,其中第$i$行第$j$列的值$D_{ij}$ $(D_{ij} = D_{ji}, D_{ii} = 0)$表示城市$i$与城市$j$之间直接相连的那条道路的灰尘度。
接下来$n$行,每行包含$n$个整数,相邻两个整数之间用一个空格分隔,其中第$i$行第$j$列的值$L_{ij}$ $(L_{ij} = L_{ji}, L_{ii} = 0)$表示城市$i$与城市$j$之间直接相连的那条道路的灰尘度的下限值。
输出格式
输出一行包含一个整数表示答案。
测试样例
| 样例输入 | 样例输出 |
|---|---|
| 3 10 0 2 4 2 0 1 4 1 0 0 2 2 2 0 0 2 0 0 |
2 |
样例说明
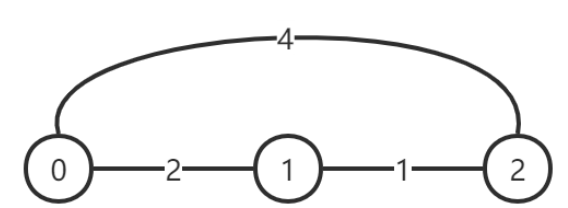
初始时的图如下所示,每条边上的数字表示这条道路的灰尘度:
此时每对顶点之间的灰尘度最小的路线对应的灰尘度为:
$$
d(0, 0) = 0, d(0, 1) = 2, d(0, 2) = 3, \
d(1, 0) = 2, d(1, 1) = 0, d(1, 2) = 1, \
d(2, 0) = 3, d(2, 1) = 1, d(2, 2) = 0.
$$
初始时的 P 指标为 (2 + 3 + 1) × 2 = 12,不满足 P ≤ Q = 10;
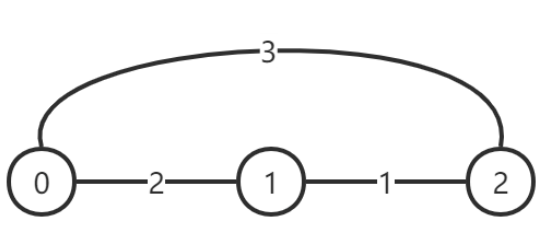
第一天,0 号城市进行道路改善,改善后的图示如下:
注意到边 (0, 2) 的值减小了 1 ,但 (0, 1) 并没有减小,因为 L0,1 = 2 ,所以
(0, 1) 的值不可以再减小了。此时每对顶点之间的灰尘度最小的路线对应的灰尘
度为:
$$
d(0, 0) = 0, d(0, 1) = 2, d(0, 2) = 3, \
d(1, 0) = 2, d(1, 1) = 0, d(1, 2) = 1, \
d(2, 0) = 3, d(2, 1) = 1, d(2, 2) = 0.
$$
此时 P 仍为 12。
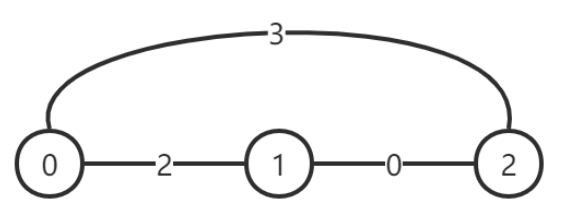
第二天,1 号城市进行道路改善,改善后的图示如下:
此时每对顶点之间的灰尘度最小的路线对应的灰尘度为:
$$
d(0, 0) = 0, d(0, 1) = 2, d(0, 2) = 2, \
d(1, 0) = 2, d(1, 1) = 0, d(1, 2) = 0, \
d(2, 0) = 2, d(2, 1) = 0, d(2, 2) = 0.
$$
此时的 P 指标为 (2 + 2) × 2 = 8 < Q ,此时已经满足条件。
所以答案是 2。
规模与约定
对于 30% 的评测用例,$1 ≤ n ≤ 10 ,0 ≤ L_{ij} ≤ D_{ij} ≤ 10$;
对于 60% 的评测用例,$1 ≤ n ≤ 50 ,0 ≤ L_{ij} ≤ D_{ij} ≤ 100000$;
对于所有评测用例,$1 ≤ n ≤ 100 ,0 ≤ L_{ij} ≤ D_{ij} ≤ 100000 ,0 ≤ Q ≤ 2^{31} − 1$。
考场思路
不得不说这个题长到离谱(其实是样例解释长),所以我最后看的这个题。这个题暴力的话显然就是每天都用Floyd算法求一遍最短路,然后求一遍P就可以了,复杂度上是$O(day \cdot n^3)$,其中Day是需要经历的天数,至于输出-1的情况,完全可以用$L_{ij}$作为边权跑一次Floyd就知道了。问题就是,这个复杂度是无法接受的,甚至连60%的数据都不能通过,只能拿到30%的分。
这里呢注意到数据规模中$n$是比较小的,但是$D-L$可能是比较大,所以考虑二分答案,理想中复杂度应该是$O(log(\frac12n(D-L))\cdot n^3)$,这样复杂度的话就很可以接受了。这里二分的话最大的天数应该是$\frac12nD=5e6$。check函数的代码大概如下(复杂度是$O(n^2 + n^3)$):
bool check(int day)
{
int turn = day / n; // 每一轮,每条道路灰尘度下降2
day %= n;
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
{
dis[i][j] = D[i][j] - 2 * turn;
if(day > i) dis[i][j]--; // 如果这一轮城市i还进行了清理
if(day > j) dis[i][j]--; // 如果这一轮城市j还进行了清理
if(dis[i][j] < L[i][j]) dis[i][j] = L[i][j]; // 注意灰尘度是有下限的
}
floyd(); P = 0;
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
P += dis[i][j];
if(P <= Q) return 1;
return 0;
}G 题:选素数
问题描述
小蓝有一个数 x,每次操作小蓝会选择一个小于 x 的素数 p,然后在 x 成为 p 的倍数前不断将 x 加 1,(如果 x 一开始就是 p 的倍数则 x 不变)。
小乔看到了小蓝进行了 2 次上述操作后得到的结果 n,他想知道 x 在一开始是多少。如果有多种可能,他想知道 x 一开始最小可以是多少,而如果不存在任何解,说明小乔看错了,此时请输出 −1。
输入格式
输入一行包含一个整数 n ,表示经过两次操作后 x 的值。
输出格式
输出一行包含一个整数表示 x 的初始值。如果有多个解,输出最小的。如果不存在解,请输出 −1 。
测试样例
| 样例输入 | 样例输出 |
|---|---|
| 22 | 8 |
规模与约定
对于 60% 的评测用例,$1 ≤ n ≤ 5000$;
对于所有评测用例,$1 ≤ n ≤ 10^6$。
考场思路
这个题的长度就和前面那个题形成了鲜明的对比😃。经过一番思考,可以发现,如果数$x=p_1^{k_1}p_2^{k_2}\cdots p_m^{k_m}$且其中$p_1 < p_2 < \cdots < p_m$,则$x$的上一个数可能且只可能位于$[x-p_m+1,x-1]$中,且如果$x$是素数,这上一个数不存在。
发现这一点之后就可以做了,只需要先把$x$质因数分解,然后找出最大的素因子,得到只经过一轮的数,然后在把所有可能的数都再进行一次操作,就可以得到所有符合要求的原始数了。复杂度应该是$O(\sum_{i=\sqrt n}^{n} \sqrt i)$,不过经过计算可知这个复杂度大约是$O(n^{\frac32})$,其实是过不了全部数据的,但是由于大部分数不是质数,都拥有较小的质因子,所以分解质因数的复杂度应当小于$O(\sqrt x)$,所以我大胆猜测是可以过的。
考试代码如下:
unsigned solve(int x, int depth)
{
if(depth == 0) return x;
if(x <= 2) return (unsigned)-1;
vector<int> prime_i; // 显然是没有必要的
int tmp = x;
for(int i = 2; i * i <= tmp; i++)
{
if(tmp % i == 0)
{
prime_i.push_back(i);
while(tmp % i == 0) tmp /= i;
}
}
if(tmp != 1 && tmp != x) prime_i.push_back(tmp); // tmp==x说明是x质数
if(prime_i.empty()) return (unsigned)-1;
int max_p = prime_i.back();
unsigned anss = (unsigned)-1;
for(int i = 1; i < max_p; i++)
{
anss = min(anss, solve(x - i, depth-1)); // 用unsigned其实就是为了取min方便
}
return anss;
}主函数调用solve(n,2)然后把返回值转化为int即可。
未完待续……
其实剩下的三个题我都不会了……😢